"1001 ночь в казино"

Победа над генератором случайных чисел (ГСЧ) своего ПК

Углубляясь в теорию игры на рулетке, я изучил большое количество известных игровых систем, но ни одна из них на длительной дистанции не имела преимущества, ни над ГСЧ  реальной рулетки, ни над ГСЧ моего компьютера.

Кроме того, часто приходилось слышать мнение о том, что способ игры на рулетке ни каким образом не влияет на конечный результат. Любая схема игры приводит к стандартному проигрышу, равному (–2,7%) от количества ставок. Мои исследования скорее подтверждали такое утверждение, чем отрицали, и тем не менее, что то мне мешало полностью согласиться с такой точкой зрения.

С одной стороны в голове никак не укладывалось, что всё неизменно должно закончиться (–2,7%), что бы мы ни «сотворили». С другой стороны, если можно было бы добиться хотя бы (–2,5%), то, что нам мешало бы добиться (–2%), (-1,5%) и, наконец, 0% или даже положительного баланса.

Известно, что кривая игрового баланса не линейная функция, с асимметричной мало предсказуемой синусоидальной траекторией (неизменно отрицательным является лишь  тренд, который собственно и составляет эти (–2,7%) и постепенно уводит все волны функции под ось абсцисс). Таким образом функцию игрового баланса можно разделить на две составляющие: синусоидальную, всегда стремящуюся к "0", и прямую с коэффициентом (-2,7), стремящуюся к минус бесконечности. Очевидно, что только в синусоидальной составляющей нужно искать рациональное зерно. Руководствуясь этим я попытался сформулировать гипотезу, с помощью которой можно было бы создать систему с МО отличным от (–2,7%). Звучит она так: 

Если волна есть, то ее можно поймать

Потратив много времени на изучение поведения игрового баланса, я пришел к выводу, что присущая ему волнообразность распознаваема и классифицируема. Особенно характерным показателем волны является ее амплитуда. Собственно, главное во всем этом - это именно наличие самой волны. Следовательно умение поймать волну -  путь для достижения успеха. Приведу пример, как можно это использовать. 
Возьмем 10-12 чисел выпавших на рулетке за 12 последовательных спинов, и будем отслеживать их дальнейшее появление на протяжении 250 бросков. Если наложить друг на друга тысячи таких отрезков, то получим график типа: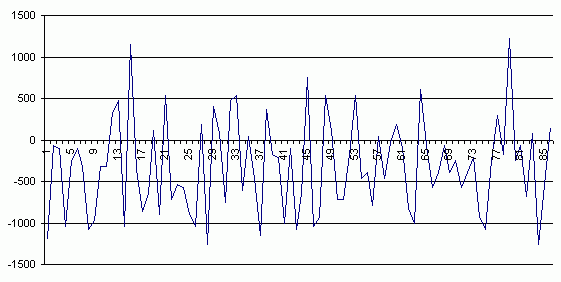
Из графика видно, что группа определенных чисел время от времени выпадает, то реже, то чаще. Максимумы пиков графика тоже не равны. Это позволяет сделать предположение, о неравновероятности ожидания повторного появления  заданных чисел на различных участках. Естественно, нас интересует интервал их максимально вероятного появления. Это и есть искомая нами волна. Такой интервал был мной экспериментально найден.
Существенной особенностью волнового процесса выпадения номеров на рулетке является отсутствие у волны четкой периодичности, что собственно и является главной трудностью при построении большинства систем. Но если параметры волн одиночных экспериментов практически непредсказуемы, то волна, полученная наложением тысяч одиночных экспериментов, ведет себя более устойчиво и ее максимум можно привязывать к определенным числам (спинам).

Тем не менее, на практике, когда мы имеем дело с конкретными одиночными волнами, нам надо это учитывать при построении работоспособной системы. Здесь применимо следующее предположение. В реальном единичном прогоне системы, выбранная нами группа чисел может выпасть на конкретных (выявленных экспериментальным путем) спинах, а может и не выпасть. Но на расширенном интервале спинов, включающих оптимальный интервал и некоторое количество спинов ранее, такая вероятность гораздо более высока. В связи с этим, нам надо лишь быть уверенными, что на интервале предшествующем оптимальному, интересующая нас группа чисел не выпадала (т.е. волна не отклонилась от оптимальной частоты), тогда вероятность появления ее на оптимальном интервале станет максимальной, и мы должны это использовать.
Благодаря такому подходу в ходе компьютерной реализации данной идеи мне реально удалось, ожидая числа на отдельных конкретных спинах, достичь устойчивых значений игрового баланса значительно меньших (-2,7%), а в отдельных случаях и вовсе положительного результата.

Другой работоспособной гипотезой я считаю:

конечность маловероятных событий

То есть, на практике «шанс» не может падать бесконечно, хотя с одной стороны, и имеет, при каждом новом броске одинаковую вероятность с противоположным. Рано или поздно смена шанса происходит, и это «рано или поздно» имеет вполне реальные цифры. Так, например, после 11 раз повторения шанса, вероятность выпадения противоположного шанса близка к 50 процентам с учетом возможности выпадения «0». Смотри файл

Интересных результатов мне удалось добиться при таком экзотическом исследовании, как количество возможных повторов комбинации «ММББ» после конкретных различных чисел. Так после «1» ставить на «Большие» оказалось на 6,5% выгоднее, чем на «Малые», после 7 выпадений в подряд комбинации «ММББ», и на 22,8% выгоднее после 8 выпадений этой комбинации.

Характерно то, что при исследовании других чисел результаты достаточно сильно отличались от вышеописанных, что говорит о несовершенстве функции ГСЧ программы «Эксел». Но кто сказал, что реальная рулетка – это совершенный генератор. Имею смелость предположить, что нет. Хотя, чтобы строить достоверно работоспособные системы на основе реальных спинов, надо иметь под рукой сотни миллионов таких спинов.

Тем не менее, так или иначе, мне удалось обыграть ГСЧ своего компьютера, хоть это и стоило мне больших сил и фантазии. Кроме того мне удалось обнаружить и другие пути решения задачи, и реализовать их. Но в реальной игре такие системы все же мало применимы, потому, что выиграть одну фишку за 1000 спинов для игрока в рулетку все равно, что не играть вовсе.

при использование материалов сайта - ссылка на источник обязательна